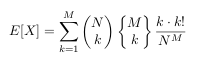March Madness bracket with integer programming in Python
4-13-15
In this IPython notebook I explore the use of an integer program solver in Python to pick an optimal March Madness bracket. (An integer program is an optimization problem where the variables are constrained to be integers)
notebook
github
Logistic regression with binomial data, in python
1-25-15
Scikit-learn's batch logistic regression doesn't support a binomial response -- where your data is (successes, trials) rather than (success or failure). This can be a drag when you have a lot of trials with the exact same features, as your design matrix will be repetitive and much larger than necessary.
It isn't too bad to do it yourself without scikit-learn though, which I show in
this short IPython notebook.
Better use of prior information in Bayesian AB testing
6-14-14
You might not know in advance precisely what your conversion rate will be, but you do know that
changing a button from green to blue isn't going improve it from 0% to 100%. Your statistical model can (easily)
and should use that knowledge, and it makes a big difference.
Read all about it.
Heatmap of UFO sightings
5-25-14
There's a lot of stuff for this one, read the full article.
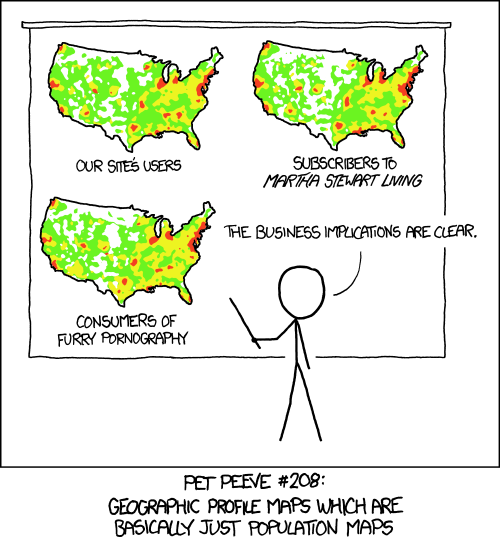
Going from this

which looks a lot like this
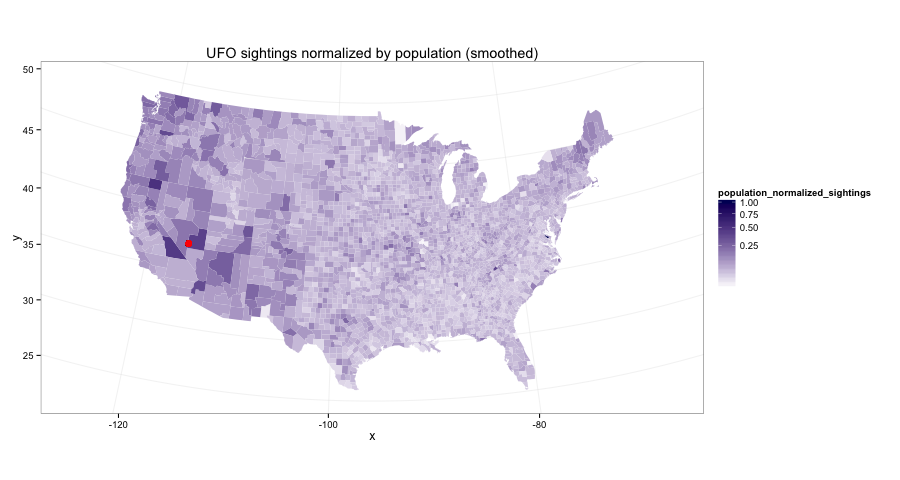
and doing the work to get to this
Wikipedia link graph, MapReduce, PageRank
12-1-12
As an excuse to play with some Amazon Web Services credit
($100) I got from a class, I decided to mess around with the Wikipedia
link graph. The main file expands to 20GB+ and is in an
inconvenient format, and so Amazon's Elastic MapReduce was a useful
tool to parse it in a reasonable amount of time and build the
graph.
The files:
- enwiki-latest-pagelinks.sql.gz -- Contains most of the
information needed to build the graph. It's a MySQL dump where
rows contain triples of the form (from page ID, namespace, to
page name). Annoyingly, the "to pages" are given with their
text name which needs to be converted to an ID. The next file
includes the necessary info to do the mapping. We are only
concerned with the "Main" namespace; the others (e.g. Talk and
Help pages) should be discarded.
- enwiki-latest-page.sql.gz -- Contains information for each
page, in particular both its text name and integer ID.
I launched an EC2 instance, downloaded the files, unzipped them,
then pushed them onto S3. The pagelinks.sql file is so large that
this wasn't completely straightforward. I ended up using boto to push it up in smaller
2GB chunks.
With the graph built, it's a pretty staightforward task to
build the in and out degree distributions. For fun, I used EMR to
do this as well, though it's a simple enough task to run on single
machine. I should include some comments and graphs on the
distributions here. (UPDATE: I did this, see below)
Next I tried for each page to compute the top ten most similar
pages based on out-link structure. I failed to do this, and gave up
after exhausting my $100 budget. It's a tough task to parallelize,
and similar to k-nearest neighbors in that each subtask needs to
know the whole graph. I've read of clever ways to combat this, e.g.
locality-based hashing, but didn't get around to implementing any.
The next step is PageRank, a fairly straightforward linear
algebra problem. This can be parallelized easily (just matrix-vector
multiplication) but needs to chain together multiple MapReduce tasks.
I couldn't find a simple way to do this within the EMR framework,
though I bet there is a way to do it.
The wikipedia graph is small enough, however, that it might fit
into memory on a single machine. I haven't gotten around to doing
this yet.
UPDATE
The wikipedia graph does indeed fit into memory, 2GB as a
sparse matrix in scipy. I implemented PageRank and played with it a
bit, nothing too exciting. I should put together a graph or table
or something. (UPDATE: I did this, see github link below)
Also, I am told that Pig is a good tool for doing high-level
mapreduce jobs and it can be used on AWS. I should look into that.
UPDATE 12-30-13
Luke Stanley
actually needed to use this for a real purpose. I helped him out;
see some results and discussion on
github.
Includes some
graphs
on the inlink and outlink distributions for the Tagalog wikipedia.
Travelling Salesman Problem (TSP)
6-9-12
Given a list of cities and their pairwise distances, the task is
to find the shortest possible route that visits each city exactly
once and returns to the origin city
A colleague of mine had recently learned a simulated annealing approach
to approximately solving this which he bragged about. I scoffed, telling
him I could solve it exactly, and much faster. I was wrong at first, but
after a year I did learn all the necessary pieces.
cutting-plane method
I used the cutting-plane method (described pretty well above) using a Columbia CS
student's code
to find the mincuts, and gurobi to solve the integer program. 50ish lines of python
outside of those two subroutines, and really fast for 20 cities, less than a tenth
of a second typically.
github
Balls and bins
3-28-12
My friend Chris posed this problem:
Imagine an array of N cups. High above the cups you drop M ping
pong balls, so that the probability of a ball entering any cup is
totally uniform.
What is the expected number of occupied cups (or empty cups,
whatever)? Assume each cup is big enough to hold all M balls
should they all fall in one.
Application:
When I worked on a medical imaging device, we used these things called
solid state photo multipliers. The way it works is exactly analogous
to dropping in M photons into N boxes and counting the non empty boxes.
We always assumed that K non-empty boxes implied K incident photons
(which is a solid approximation for M << N), but I was always curious
about how to account for saturation effects once M ~ N.
My answer:
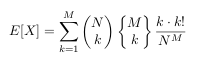
solution (pdf)
UPDATE
My solution is way too complicated. There is a much easier way
to go about it by using the linearity of expectation; that is, the
expected number of non-empty cups is simply the sum over all cups
of the probability that a particular cup is non-empty (since the
cups are independent). It also allows a simple answer to the
follow-up question: what is the limit as N goes to infinity of E[#
bins filled from N balls in N bins]/N ? Both the simpler solution
and the follow up question are left as an exercise for you. (It really
is pretty straightforward and satisfying, try it.)
Instagram Challenge: Unshredder
11-15-11
Given an image randomly sliced into vertical strips, can you piece back
together the original?
The challenge
github

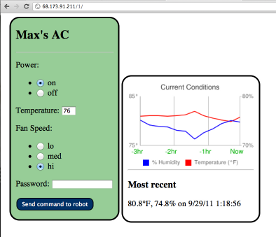
Mobile air conditioner control
Summer 2011
Control your air conditioner via website. Arduino project #1
website
github
Independent Chip Model (ICM)
2004
How valuable are the different stacks in a poker tournament with a
top-heavy payout structure? How does this influence strategy?
twoplustwo magazine article reposted on some German poker blog.
I got paid $200 to write this in college, which made me feel pretty cool.
It's been linked around quite a bit and even cited in a super detailed
analysis of the value of a chip in a tournament, in Japanese.
Original post on twoplustwo forums
github